El Saiens, el Coiens y el Adsust

Imagen I: Un fragmento del alfabeto de un lenguaje saiens de tipo 1, por Jakeukalane.
Texto original de Avengium inspirado en la utilización por parte de los científicos de la simbología matemática de sus respectivas ciencias. Ver nota.
0. Introducción.
1. El Saɪəns de tipo 1.
2. El Saɪəns de tipo 2.
3. El Coiens.
4. El Adsust.
El lenguaje es una manera de expresar las percepciones y los conocimientos. Gracias a un lenguaje estructurado podemos estructurar nuestro conocimiento de la realidad y la ficción y comunicar nuestros pensamientos y percepciones con los demás. Un lenguaje es importante para el avance de la cultura y un lenguaje matemático robusto es importante también para el avance de la ciencia.
Una rama de esos lenguajes matemáticos que han ayudado tantas veces al avance de la civilización es la rama del Saɪəns o Saiens (pronunciado /sa-ɪəns/) o lenguajes Saiens.
Muchas especies a lo largo del Milegu han nombrado a sus lenguajes como Saɪəns u otros nombres similares o derivados. De entre estos, el más destacable es el que han desarrollado los Cogi. Aunque otros Saiens como el que se dio en una Tierra Neshl en el que los humanos migraron de la tierra y después volvieron encontrándola irreconocible (la Tierra Extraña) también es popular en algunos lugares.
La complejidad o robustez de un lenguaje Saɪəns tiene diferentes grados, a más robusto, mayor en la escala. El más común es el Saɪəns de tipo 1.
Los lenguajes matemáticos de este nivel son sencillos y se trabaja de manera intuitiva. En este nivel quien los diseña procura que los símbolos científicos a los que hace referencia cada concepto no se repitan. Esto lo hace reuniendo todo el compendio de símbolos del idioma y comprobando que no haya dos repetidos.
En caso de que dos o más conceptos, fuerzas, partículas u otras cosas compartan un mismo símbolo a la hora de ser representadas, el diseñador de este lenguaje crea nuevos símbolos para cada concepto, o añade una modificación o serifo al símbolo inicial por cada concepto para diferenciar los conceptos haciendo sus símbolos únicos.
Ejemplo de múltiples conceptos con el mismo símbolo:
- En física, V representa la velocidad de un cuerpo en movimiento.
- En química, V es el símbolo del vanadio.
- En bioquímica, V es el símbolo del aminoácido valina.
- En electricidad, V es el símbolo del voltio, unidad en la que se mide el potencial eléctrico, que también se representa por V.
Otro ejemplo de múltiples conceptos con símbolo igual:
- En física, U, en mayúscula, es el símbolo del uranio.
- En física u, en minúscula, es el símbolo de la antiguamente llamada unidad de masa atómica (uma).
- En termodinámica, U es el símbolo de la energía interna.
- En la bioquímica, U es la unidad de actividad enzimática.
Así, creando símbolos distintos para cada concepto, se reduce la ambigüedad de los enunciados y los conceptos no se confunden unos con otros debido a sus símbolos.
En una amplia mayoría de los planetas y regiones del cosmos en las que se han inventado lenguajes Saɪəns, se observa con posterioridad, que esas civilizaciones experimentan una aceleración en su desarrollo cultural y científico.
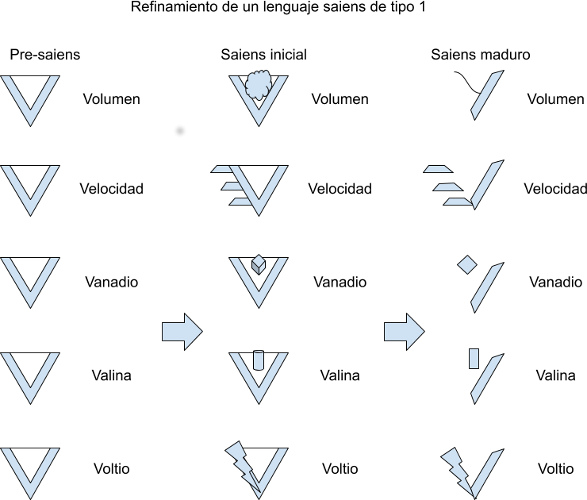
Imagen II: Refinamiento de un lenguaje saiens de tipo 1, por Avengium.
Debido a la relativa artificialidad de estos lenguajes creados, las sociedades que los usan conservan un glosario con todos los términos y símbolos. Sorprendentemente, muchas de estos glosarios se parecen entre sí, lo que indicaría que su origen es común o que hay una convergencia al usar los mismos símbolos en distintas partes del cosmos. Lo que apunta a un posible entendimiento de especies rotundamente distintas.
A pesar de esta convergencia (aparente o no) en los lenguajes Saɪəns, cada uno es distinto, se inventó en un contexto distinto y partiendo de lenguajes diferentes. Esto hace que los lenguajes Saiens de bajo nivel no sean comparables unos con otros a pesar de ser glosarios unívocos de la ciencia de su región. Estas y otras dificultades se englobaron en algo que los expertos denominaron "teoría de la relativización de la simbología" que dice que por muchas correspondencias que tengan los símbolos Saɪəns no tienen entidad por sí mismos y son elecciones arbitrarias.
"—Ustedes los legos se equivocan al pensar que a los científicos les basta con mirar una ecuación y decir: «Ah, sí...» y luego pueden ponerse a escribir un libro sobre ella. La matemática no posee una existencia propia; no es más que un código arbitrario ideado para describir observaciones físicas o conceptos filosóficos. Cada hombre puede adaptarlo a sus necesidades particulares. Por ejemplo, nadie puede mirar un símbolo y estar seguro de lo que significa. Hasta la fecha, la ciencia ha utilizado todas las letras del alfabeto, mayúsculas, minúsculas y en bastardilla, y cada una de ellas simboliza diversas cosas. Ha utilizado letras en negrita, letras góticas y letras griegas, lo mismo mayúsculas que minúsculas; subrayados, superrayados, asteriscos y hasta letras hebreas. Científicos distintos utilizan símbolos diferentes para el mismo concepto e idéntico símbolo para conceptos distintos. De modo que si usted le enseña a uno, quienquiera que sea, una página suelta como ésa, sin darle noticia de la materia investigada ni de la simbología particular empleada, la persona en cuestión no le hallará ningún sentido" 1.
Un texto que afirma que la "teoría de la relativización de la simbología" se cumple para cualquier lenguaje simbólico.
Pero en el Milegu hay multitud de especies más avanzadas que aquellas que sólo conocen los Planos Materiales. Los Cogi, los Dussianos, los Dyssianos, los Kdieua y miles más conocen la existencia de muchos otros Planos. La ciencia de estas especies llega a cotas increíbles haciendo que sus aparatos tecnológicos parezcan inexplicable magia a ojos de científicos menos avanzados.
A lo largo de su historia, los Cogi han desarrollado un formidable método científico, desarrollando lenguajes Saɪəns varias escalas superiores a los comunes. Estos lenguajes les han servido a su vez para elevarlos cada vez a cotas más altas, como el Saɪəns de tipo 2 creado por el Magíster cogi Gaux, y a desarrollar uno de los más populares lenguajes Saɪəns de tipo 2 de los Planos Materiales.
Los lenguajes Saɪəns de tipo 2 se construyen sobre los mismos principios que los Saɪəns de tipo 1, símbolos únicos para cada concepto, universalidad de los símbolos, glosario de términos, etc. Pero a diferencia de estos, los lenguajes Saɪəns de tipo 2 cuentan con mecánicas y leyes bastante oscuras que requieren de conocimientos avanzados en multitud de materias.
Debido a la nueva teoría de la simbología que se desarrolla en los lenguajes Saɪəns de tipo 2, estos son poco accesibles y apenas se usan como escritura habitual, excepto por genios o en campos directamente relacionados con esta simbología.
El lenguaje Saɪəns de tipo 2 Cogi funciona de manera distinta dependiendo de cómo se lo use. Su función más común es la de actuar como una piedra de Rosetta de lenguajes científicos y de simbologías descriptivas de todo tipo.
El Saɪəns 2 es un lenguaje multinivel y conociendo un nivel se pueden conocer los otros niveles ya que también actúa como piedra de Rosetta para sí mismo. Ciertos lenguajes de Saɪəns 1 pasan a formar parte de un Saɪəns 2 una vez se han descubierto lo que añade nuevos matices e interrelaciones entre los símbolos y hace al Saɪəns 2 en cuestión más potente.
Por esta razón los Cogi y otras razas recopilan e inventan lenguajes Saɪəns de tipo 1, con el consiguiente esfuerzo que eso significa. Y después, los someten a un análisis para encontrar sus similitudes y diferencias. Esto debilita el impacto que tiene la "teoría de la relativización de la simbología" en estos lenguajes de tipo 2.
Una vez analizados estos lenguajes, se archivan y clasifican. A partir de estos se pueden inventar otros lenguajes y aquellos que se descubran o se inventen que tengan iguales símbolos se relacionarán y las posibles diferencias se cotejarán y se archivarán también. Con toda esta información correlacionada, las especies lo suficientemente avanzadas encontrarán los patrones para la construcción de un nuevo tipo de escritura, un lenguaje Saɪəns de tipo 2.
Ver una fórmula Cogi puede inspirar muchas cosas, miedo, asco, sorpresa, éxtasis, serenidad y esa fórmula puede estar escrita de muchas formas distintas. Aunque la escritura de Saɪəns de tipo 2 pueda parecer arbitraria para los no iniciados, las marcas, las serifas, la puntuación y todos sus detalles están meticulosamente medidos para expresar cantidades ingentes de información y de él surge una de las variedades de Saɪəns 2 más refinadas y completas. Lo que les ha permitido conocer las maravillas del cosmos y llegar incluso a conocer alguno de los inaccesibles "lenguajes fundamentales del Milegu".
En el Milegu todas las posibilidades son ciertas: cierta es la teoría de la relativización de la simbología y cierta es su falsedad, cierto es que el Saɪəns permite conocer la realidad y cierto es que permite desconocerla. En el Milegu, la matemática y los demás conceptos poseen una existencia propia, una vida propia y cambiante y que influye en el cosmos de miles de maneras. Sólo hay que descubrirlas.
Durante una de sus expediciones interplanares para encontrar la fuente de cierta variedad de Saɪəns de tipo 1, los Cogi llegaron a un lugar exótico y cargado de poder. En este plano, enormes símbolos multidimensionales flotaban ingrávidos, suspendidos por el Tejido de la Realidad. Esta fue la primera vez que vieron los Simbjetos.
Estos símbolos tenían cierta semejanza con algunos de los símbolos Saɪəns más extraños y cargados de simbolismo metafísico de su repertorio. El alto grado de desarrollo de su ciencia les permitió descifrar el primer Simbjeto que se encontraron. Descubrieron que estos Simbjetos, parecidos a laberínticos politopos tenían relación con el Aiúa del que hablan los Daren’Ga, con las esencias y con la definición fundamental de las cosas. Un grupo de scienticos de los Cogi Verdes examinó el Simbjeto y descubrió que había una cantidad infinita de Simbjetos, cada uno definiendo a un ente. Aún a día de hoy, su análisis continúa.
El Coiens es un lenguaje fundamental que ha sido descubierto muchas veces por muchas criaturas, en muchos tiempos distintos. Todos los lenguajes fundamentales aspiran a describir el cosmos y el Coiens (también llamado de muchas otras maneras a lo largo de la historia) lo intenta mediante símbolos.
Cada símbolo corresponde a un único ente del cosmos. Por cada ente, en el Coiens existe un símbolo distinto. Cuanto más se parecen dos entes, más se parecen los símbolos que los representan.
Cuando se habla del Coiens, normalmente se está haciendo referencia al lenguaje fundamental que descubrieron los Cogi. Mucho después de tener un lenguaje Saiens ampliamente consolidado, tanto el Coiens como el Saiens se parecen en sus aspectos iniciales. Pero cuando nos adentramos en sus complejidades, las diferencias se hacen notables. Mientras el Saiens es usado para describir la realidad física, en Coiens existe como el nombre fundamental de los entes en el cosmos. Los símbolos del Coiens no son solo símbolos impresos, sino que son símbolos vivos y poliédricos. Sus representaciones flotan en el espacio y son llamadas Simbjetos 2. Estos Simbjetos son esferas multidimensionales con patrones escritos y labrados, oquedades y protuberancias, cambios en la textura y el color. Todos estas características son las que hacen a cada Simbjeto un símbolo-objeto único.
El Coiens no ha mostrado nunca tener limitaciones a la hora de describir el cosmos y todos las anteriores limitaciones que encontró cada especie eran más bien limitaciones de esa especie antes que retricciones del Coiens. Cuando uno de estos seres percibe que uno o varios simbjetos le intentan comunicar algo, pero él no logra encontrar el término para describirlo, se dice que ese ser está bajo la influencia del Adsust 3 o que tiene una dificultad adsústrica. Esto quiere decir que el lenguaje de destino no tiene un término para describir el concepto o ente que revela el Coiens y de ahí la sensación de inefabilidad. Algunos estudiosos dicen qué qué cuando un ser siente muchas cosas distintas a la vez, cuando se siente conectado con el cosmos o cuando se está en un estado similar al Numuruing 4, es muy probable que ese ser tenga una dificultad adsústrica para definir su sentimiento global.
En el Milegu hay una gama infinita de cosas para llenar todo un lenguaje verbal. Con lo que se habrá llegado al límite de practicidad de ese idioma sin agotar el número de cosas por nombrar. Asimismo, el mismo objeto, ente, idea o criatura tendrá diferentes nombres en diferentes Planos de existencia. Y debido a que hay infinitos Planos, a cada objeto o idea se le dará una sucesión infinita de nombres distintos aún siendo lo mismo y nombres iguales para objetos distintos. Como muestra, este pequeño ejemplo para el objeto "vegetales": Ej: vegetales, veigetales, vegetailes, vegeitales, viegetales, vaiegetales, vegetiales, vegeitiales, etc. Y así hasta el infinito. Cuántos más Planos se conocen, más riesgo hay de caer en el Adsust.
Al igual que el Coiens tiene similitudes iniciales con el Saiens, también las tiene con multitud de otros lenguajes, con las runas, las yggdrunas, los lenguajes de poder, la magia basada en el lenguaje, el Arkanens producido por los Drag’Hunn y otros.
Los Coleccionistas de sonidos también estudian el Coiens, ya que este da un simbjeto a cada sonido que existe en el Milegu. Los Coleccionistas de sonidos dan a este lenguaje el nombre de "el alfabeto Infinito".
El fin último de todos los que estudian o estudiaron Coiens en algún momento de la historia siempre ha sido la comprensión total y el Coiens también tiene un símbolo para esto. Se llama el Simbjeto más perfecto de Todo y se dice que en él está recogido y no recogido todo el Milegu. Por supuesto, el Simbjeto más perfecto de Todo es un ente que tiene reminiscencias de la Figura más perfecta de Todo, aunque no sea la Figura más perfecta de Todo ni pueda serlo. Es decir, está relacionado con la Figura mediante la Multiplicidad de lo Único. Frente a él, el grado de Adsust de una criatura será infinito y solo aquellas que no tengan Adsust podrán descifrarlo y comprender sus secretos.
*1: La cita procede del relato "La carrera de la Reina Roja" de Isaac Asimov. Volver.
*2: Este nombre es una combinación de las palabras símbolos, objetos. Volver.
*3: Adsust tiene las palabras "adjetivo", "sustantivo", "aditivo", "sustractivo". Volver.
*4: El Numuruing es un estado de ánimo meláncolico propio de los seres que viajan entre Planos). Volver.
Nota I: La teoría de la relativización de la simbología está inspirada en el relato "The Red Queen’s Race" (1949) de Isaac Asimov traducido en español como: "La carrera de la Reina Roja (PDF)". El párrafo que habla sobre la teoría de la relativización de la simbología está directamente extraído del relato de Asimov.
Criaturas: Cogi, Cogi Verdes. Dussianos, Dyssianos, Kdieua, Daren’Ga, Drag’Hunn, Coleccionistas de sonido.
Espacios Planares: Milegu. Tierra Neshl, Tierra Extraña, Planos Materiales. Tejido de la Realidad.
Estructuras Finales: Figura más perfecta de Todo.
Conceptos: Multiplicidad de lo Único, Esencias, teoría de la relativización de la simbología. Numuruing. Aiúa, Simbjetos, Simbjeto más perfecto de Todo, Coiens, Adsust, Arkaens.
Técnicas: magia basada en el lenguaje.
Idiomas: Lenguajes Saiens: Saɪəns de tipo 1, Saɪəns de tipo 2, lenguajes fundamentales del Milegu, Alfabeto infinito, runas, yggdrunas, lenguajes de poder.
Títulos: Magíster, scienticos.
Individuos: Gaux.
Conceptos reales: velocidad, vanadio, valina, voltio, uranio, unidad de masa atómica, energía enterna, actividad enzimática, politopo.
Texto: Avengium.
Imagen I: Jakeukalane.
Imagen II: Avengium.
©Avengium ©Hyposs Productions.


0 comentarios